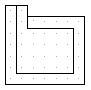
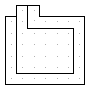
Polystrips
On this page I present results of my first attempt to count polystrips.
For simplicity I don't rotate or reflect pieces. The number of polystrips in all
positions T(n) is given in the table below.
We can count two subsets of polystrips and two supersets :
Two-directional polystrips

The number of 2dir polystrips is
L2(n) = 2n - 2
Three-directional polystrips
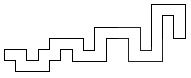
The number of 3dir polystrips is
L3(n) = c1 x1n + c2
x2n + c3 x3n - 2n
where xi are roots of x3-2x2-1=0
x1=2.20556943040059
x2= -0.10278471520030 + 0.66545695115281 i
x3= -0.10278471520030 - 0.66545695115281 i
and
c1=1.26798014703815
c2=0.36600992648092 + 0.54201687825554 i
c3=0.36600992648092 - 0.54201687825554 i
The asymptotic behavior is
| lim L3(n)/L3(n-1) = x1 = 2.20556...= |
Paths on square grid
Their number is
U0(n)=2 3n-2
Paths on square grid without sharp U-turns
Their number is
| U1(n)= |
Number of polystrips
L2(n)<=L3(n)<=T(n)<=U1(n)<=U0(n)
If the following limit exists then
| 2.205569... <= lim T(n)/T(n-1) <= 2.414214... |
Similar estimates was found for polyminoes [Klarner's constant]
| 3.91336 <= lim A(n)/A(n-1) <= 4.649551 |
| psc | T(n) | T(n)/T(n-1) | L2(n) | L3(n) | T(n) | U1(n) | U0(n) | |||
| 2 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | |||
| 3 | 2 | 6 | 3.000 | 6 | 6 | 6 | 6 | 6 | ||
| 4 | 3 | 14 | 2.333 | 14 | 14 | 14 | 14 | 18 | ||
| 5 | 7 | 34 | 2.429 | 30 | 34 | 34 | 34 | 54 | ||
| 6 | 13 | 82 | 2.412 | 62 | 82 | 82 | 82 | 162 | ||
| 7 | 30 | 194 | 2.366 | 126 | 194 | 194 | 198 | 486 | ||
| 8 | 65 | 462 | 2.381 | 254 | 454 | 462 | 478 | 1458 | ||
| 9 | 153 | 1094 | 2.368 | 510 | 1054 | 1094 | 1154 | 4374 | ||
| 10 | 346 | 2590 | 2.367 | 1022 | 2430 | 2590 | 2786 | 13122 | ||
| 11 | 818 | 6110 | 2.356 | 2046 | 5570 | 6110 | 6726 | 39366 | ||
| 12 | 1893 | 14422 | 2.360 | 4094 | 12706 | 14422 | 16238 | 118098 | ||
| 13 | 4313 | 33938 | 2.353 | 8190 | 28866 | 33938 | 39202 | 354294 | ||
| 14 | 10067 | 79910 | 2.3545 | 16382 | 65350 | 79910 | 94642 | 1062882 | ||
| 15 | 23621 | 187674 | 2.3485 | 32766 | 147502 | 187674 | 228486 | 3188646 | ||
| 16 | 55313 | 441038 | 2.3500 | |||||||
| 17 | 129647 | 1034142 | 2.3447 | |||||||
| 18 | 303720 | 2426326 | 2.3462 | |||||||
| 19 | 711078 | 5681662 | 2.3416 | |||||||
| 20 | 1665037 | 13312246 | 2.3430 | |||||||
| 21 | 3894282 | 31137950 | 2.3390 | |||||||
| 22 | 9111343 | 72871914 | 2.3402 | |||||||
| 23 | 21290577 | 170287162 | 2.3368 | |||||||
| 24 | 49770844 | 398122698 | 2.3379 | |||||||
| 25 | 116206114 | 929561314 | 2.3348 | |||||||
| 26 | 271435025 | 2171377246 | 2.3359 | |||||||
| 27 |
My questions:
1. What is the asymptotic ratio of number of polyominoes with holes and without
holes?
2. What is the asymptotic ratio of perimeter and area of polyominoes?
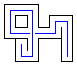
3. Polystrip and polytrees with n>=9 can't form rectangle. (The cave in the piece below
can't be filled). Polyominoes with n>=22 can't form rectangle (There are more
caves than pieces of corresponding shape). Is it possible to find similar examples
with smaler polyominoes?