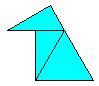
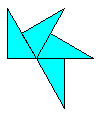

Polydrafters
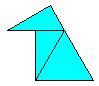
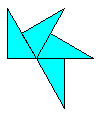

polydrafters can contain two types of holes
Tp 1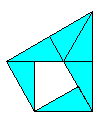
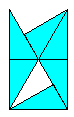 Tp 2
Tp 2
These are two representations of the same piece


Polydudes
polydudes are polydrafters without 30 deg angles, without holes and which are
not narrower then 1/4 triangle edge.
So these are not polydudes.

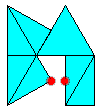
Eternity-like pieces
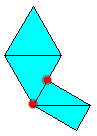
Epieces I call polydudes which are not narrower then 1/2 triangle edge.
So these are not Epieces

| Polydrafters | Polydrafters hole tp.1 | Polydrafters hole tp.2 | Polydrafters no holes | Polydudes | Epieces | ||
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | |
| 2 | 6 | 0 | 0 | 6 | 3 | 3 | |
| 3 | 14 | 0 | 0 | 14 | 1 | 1 | |
| 4 | 64 | 0 | 0 | 64 | 9 | 4 | |
| 5 | 237 | 0 | 0 | 237 | 15 | 4 | |
| 6 | 1024 | 11 | 0 | 1013 | 59 | 11 | |
| 7 | 4254 | 130 | 0 | 4124 | 152 | 14 | |
| 8 | 18664 | 962 | 0 | 17702 | 513 | 38 | |
| 9 | 81865 | 6266 | 0 | 75599 | 1539 | 71 | |
| 10 | 72 | 4993 | 179 | ||||
| 11 | 15836 | 365 | |||||
| 12 | 854 | ||||||
| 13 |
The description of file format is here. ( I am sorry for another new file format )
For alternative Eternity I decided not to use
- polyiamonds ( 854 - 12 = 842)
- symmetrical pieces ( 842 - 71 = 771 )
- grain-ambiguous piece ( 771 - 1 =770 )
Remain 770 pieces
I now that the numbers are different from results of Brendan Owens at www.mathpuzzle.com . This is probably due to different definitions or bugs. The bold numbers agrees with his results.