New Page 1

Symmetry

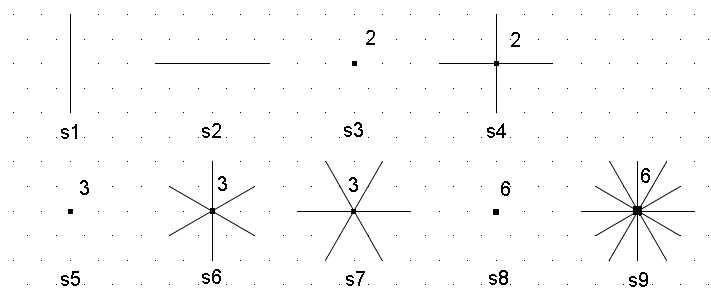
The figures can have 10 types of symmetry (s0 is no symmetry)

lines are axes of symmetry, 2 means 180 deg. rotation, 3 means 120 deg. rotation and 6 means 60 deg. rotation

Results

area	# figures	symmetry										# sides
area	# figures	s0	s1	s2	s3	s4	s5	s6	s7	s8	s9	3	4	5	6	7	8	9	10	11	12
1	3	1	0	0	1	1	0	0	0	0	0	1	2	0	0	0	0	0	0	0	0
2	8	1	0	2	3	1	0	1	0	0	0	2	6	0	0	0	0	0	0	0	0
3	11	5	0	0	3	2	0	0	0	0	1	1	7	1	2	0	0	0	0	0	0
4	17	5	2	2	5	3	0	0	0	0	0	1	11	3	2	0	0	0	0	0	0
5	21	11	1	1	4	3	1	0	0	0	0	0	8	7	6	0	0	0	0	0	0
6	31	10	5	4	9	2	0	0	1	0	0	2	16	5	8	0	0	0	0	0	0
7	33	19	2	2	6	4	0	0	0	0	0	0	9	11	11	1	1	0	0	0	0
8	45	24	3	4	8	5	0	1	0	0	0	2	19	6	14	4	0	0	0	0	0
9	52	35	1	2	9	4	0	0	0	0	1	1	12	12	22	4	1	0	0	0	0
10	63	33	7	7	13	3	0	0	0	0	0	0	15	14	25	6	3	0	0	0	0
11	72	52	2	3	9	5	0	1	0	0	0	0	9	23	27	9	4	0	0	0	0
12	91	57	5	7	15	6	0	0	0	0	1	1	30	10	31	13	6	0	0	0	0
13	96	72	5	4	11	4	0	0	0	0	0	0	9	21	37	23	6	0	0	0	0
14	120	81	9	9	17	4	0	0	0	0	0	0	16	23	45	23	11	1	1	0	0
15	134	99	5	6	15	8	1	0	0	0	0	0	18	25	53	22	16	0	0	0	0
16	150	106	9	9	18	8	0	0	0	0	0	1	24	23	48	34	18	2	0	0	0
17	170	141	4	5	14	5	1	0	0	0	0	0	9	30	66	42	20	3	0	0	0
18	203	145	12	15	25	5	0	1	0	0	0	2	26	26	68	46	29	4	2	0	0
19	209	166	10	7	20	6	0	0	0	0	0	0	8	37	70	53	34	5	2	0	0
20	245	200	8	8	19	9	1	0	0	0	0	0	27	31	70	63	46	8	0	0	0
21	272	225	7	9	22	8	0	0	1	0	0	0	19	32	90	81	41	6	3	0	0
22	305	235	20	17	30	3	0	0	0	0	0	0	16	41	88	82	62	14	2	0	0
23	333	281	8	12	21	8	1	2	0	0	0	0	12	51	101	91	61	15	2	0	0
24	376	302	14	14	32	12	0	0	1	0	1	2	46	24	93	108	75	24	3	0	1
25	385	339	9	7	23	7	0	0	0	0	0	1	10	28	123	116	84	17	6	0	0
26	453	382	14	19	31	6	0	1	0	0	0	0	16	44	122	129	101	33	8	0	0
27	482	411	16	13	32	9	0	0	0	0	1	1	17	50	140	130	109	27	7	1	0
28	517	441	18	17	33	8	0	0	0	0	0	0	29	38	125	148	121	49	7	0	0
29	577	515	11	13	28	8	2	0	0	0	0	0	8	56	144	181	129	46	12	1	0
30	648	544	26	25	45	8	0	0	0	0	0	0	34	42	158	158	178	63	14	0	1
31	642	564	15	17	36	10	0	0	0	0	0	0	9	63	144	193	177	38	17	1	0
32	745	667	15	17	33	12	0	1	0	0	0	2	32	50	150	205	200	87	18	1	0
33	786	709	15	16	35	9	1	0	1	0	0	0	19	53	175	250	193	74	20	2	0
34	858	742	29	29	52	6	0	0	0	0	0	0	16	55	170	241	243	105	25	2	1
35	902	822	19	15	36	9	1	0	0	0	0	0	14	58	206	271	222	94	35	2	0
36	1001	892	21	24	49	14	0	0	0	0	1	1	49	52	183	247	291	142	30	5	1
37	1007	920	19	18	41	9	0	0	0	0	0	0	9	54	192	312	285	120	32	2	1
38	1172	1060	27	29	49	6	1	0	0	0	0	0	15	69	199	321	354	158	52	4	0
39	1191	1073	22	26	53	16	0	1	0	0	0	0	19	74	225	357	306	154	49	6	1
40	1279	1164	29	24	50	12	0	0	0	0	0	0	40	45	207	326	389	208	61	3	0
41	1364	1279	13	21	42	7	1	1	0	0	0	0	9	65	239	407	390	191	52	10	1
42	1516	1363	38	38	66	10	0	0	1	0	0	0	35	63	238	407	424	253	88	5	3
43	1486	1371	31	24	52	8	0	0	0	0	0	0	8	64	271	395	448	221	64	15	0
44	1701	1589	19	25	51	15	0	2	0	0	0	0	29	79	242	408	517	329	83	11	3
45	1751	1614	29	30	62	14	1	0	0	0	1	0	28	68	282	472	555	228	105	12	1
46	1896	1725	47	45	73	6	0	0	0	0	0	0	19	69	276	456	583	356	119	17	1
47	1942	1817	26	29	53	14	2	1	0	0	0	0	12	103	284	521	569	323	113	14	3
48	2122	1968	32	35	67	19	0	0	0	0	1	1	60	69	245	495	671	420	143	15	3
49	2119	2004	25	23	57	10	0	0	0	0	0	1	11	48	275	634	623	360	140	26	1
50	2447	2284	39	42	72	8	1	1	0	0	0	2	21	60	323	568	755	515	177	21	5

It's easy to prove that there are no s8 figures.